Mathematik

Die Mathematik und die Kristallkugel

''Die Mathematiker sind eine Art Franzosen: Redet man zu ihnen, so übersetzen sie es in ihre Sprache, und dann ist es alsobald ganz etwas anders.'' (Goethe)

''Seit die Mathematiker über die Relativitätstheorie hergefallen sind, verstehe ich sie selbst nicht mehr.''(Einstein)

Jetzt etwas sachlicher:

''Wenn man ein mathematisches Problem von seinem konkreten Kontext löst und es mit abstrakten Symbolen und Zeichen beschreibt, dann steht die Gleichung auf einmal für sich selbst. Sie muss sich nicht mehr auf ein Problem der realen Welt beziehen, sondern beschreibt nur noch einen Zusammenhang zwischen abstrakten Größen. Daraus kann man neue Eigenschaften dieser Größen ableiten und neue Zusammenhänge finden, die dann – wenn auch nicht zwingend – wieder auf Probleme der realen Welt angewandt werden können.'' (Freistetter)

Das trifft den Kern der Sache, sagt uns aber nichts darüber, wofür das alles gut ist. Berücksichtigt man aber Angst, Eitelkeit und Machthunger, oder positiver: Wissensdurst, dann wird es sofort klar: Der Mensch will die Zukunft vorhersagen.

Dazu muß man auch Erklärungen haben, wie und warum etwas in der Vergangenheit geschehen ist. Der Mensch hat dafür nicht die besten Voraussetzungen. Das liegt daran, dass das Gehirn sich nur drei Größen wirklich vorstellen kann:

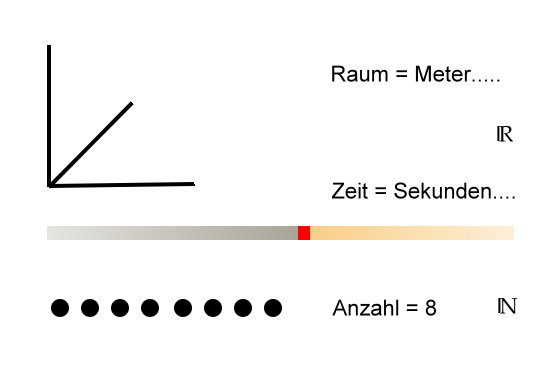
1,82 m oder 2,5 km sind Größen, mit denen man unmittelbar etwas anfangen kann, genauso wie 2 Stunden oder 10 Sekunden. Ebenso hat man eine unmitttelbare Vorstellung, wenn man weiß, dass 8 Gäste kommen oder der Karton 10 Eier enthält. Beim Letzteren handelt es sich um die sogenanten natürlichen Zahlen (IN), bei den beiden anderen um die reellen (IR). Natürlich und reell, nicht umsonst heißen sie so.

Von Begriffen wie Geschwindigkeit, Beschleunigung, Kraft, Energie oder Leistung haben wir zwar Vorstellungen, die sind aber äußerst weich und unpräzise. Oder wissen Sie wirklich genau, was der Unterschied zwischen der Leistung von 130 KW und dem Drehmoment von 450 Nm für ihr Auto bedeutet? Die Mathematik und die Physik machen aus diesen Größen Begriffe, die so genau sind, dass man sie in Formeln verwenden kann, aber meist mit unserer Vorstellung nicht mehr übereinstimmen. Erstaunlich ist, dass wir Menschen in der Lage sind, so eine Wissenschaft zu erfinden und auch noch sehr erfolgreich anzuwenden?

Fangen wir wieder einmal ganz langsam an. Mit einem Beispiel.

Ein Rad rollt auf einer Ebene. Wir haben eine Uhr und ein Maßband. Die Uhr zeigt uns die abgelaufenen Sekunden (sec) und das Maßband die Entfernung von einem Anfangspunkt in Metern (m). Wenn wir uns geschickt anstellen, können wir genau feststellen, wo sich das Rad nach einer bestimmten Zeit befindet.

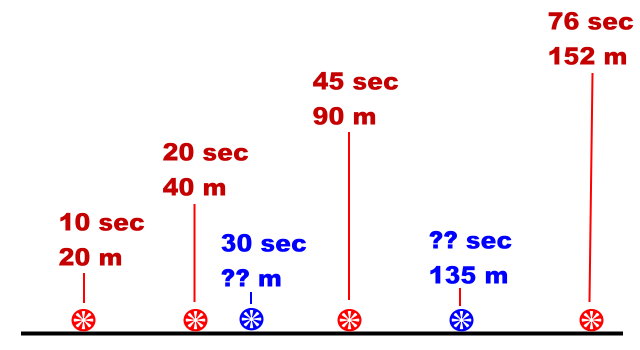
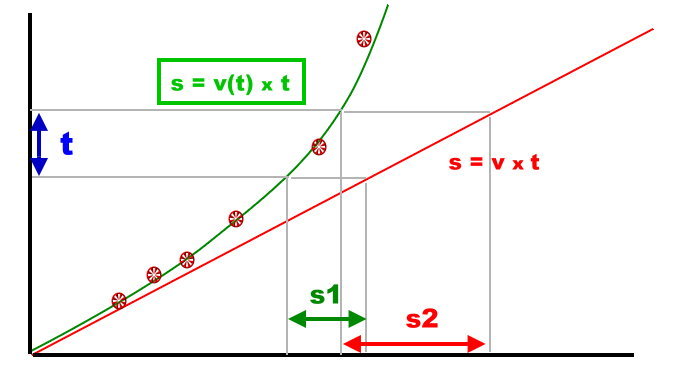
Ganz interessant wäre es, wen man auch wüsste, wann das Rad eine bestimmte Stelle erreicht, oder wo es nach Ablauf einer bestimmten Zeit ist (blaue Räder in der Zeichnung). Bekommen wir so nicht heraus. Das kann man drehen und wenden, wie man will.

Deswegen tragen wir unsere Messergebnisse ein bisschen anders auf. Wir machen ein Diagramm. Senkrecht tragen wir die Zeit auf und waagrecht den Weg wie vorher.

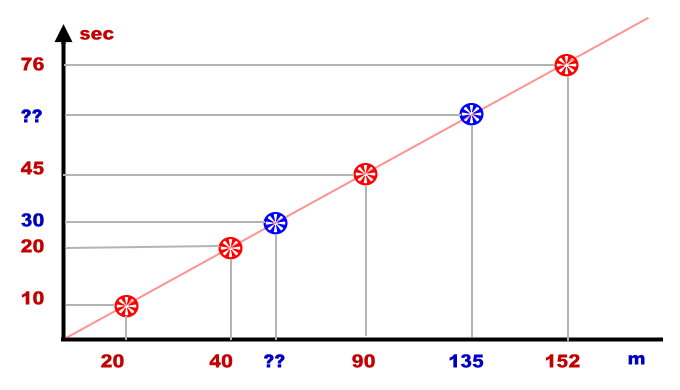
Wir sind redlich erstaunt über das Bild. Die Räder liegen alle auf einer geraden Linie. Wenn wir auf das Verhältnis der ursprünglichen Werte schauen, in dem wir den Weg durch die Zeit teilen, dann fällt uns schnell auf, warum das so ist. Es kommt nämlich immer 2 heraus: 20/10 = 2, 40/20 = 2, 90/45 = 2 und 152/76 = 2.
Jetzt, mit dieser Erkennnis und wirklich erst jetzt, können wir ganz einfach sagen, wann das blaue Rad wo ist. Wir können das aus dem Diagramm ablesen oder einfach mit Dreisatz rechnen. Setzen wir für das Fragezeichen ein x ein, dann gilt demnach 135/x = 2 oder im anderen Fall: x/30 = 2.
Das kann man auch im Diagramm 'ganz abstrakt' so darstellen:

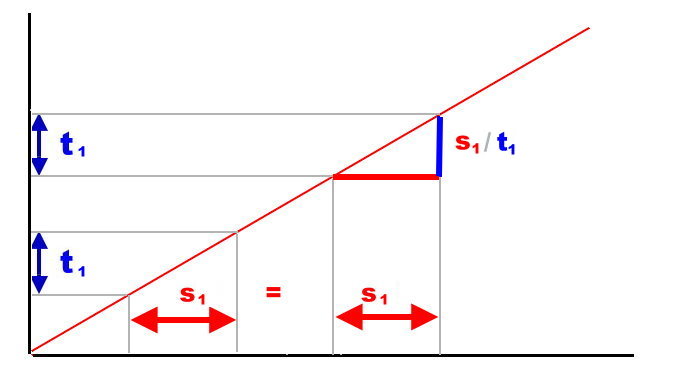
Für die gleiche Zeit (t1) ist die Strecke auch immer gleich (s1). Das Dreieck ist an jeder Stelle gleich. Wenn wir eine andere Zeit oder Strecke nehmen, eine 'beliebige', dann brauchen wir nur die Hilfe der Schulgeometrie um zu wissen, dass das Seitenverhältnis immer gleich bleibt (ist übrigens der Strahlensatz, den schon die alten Griechen kannten):

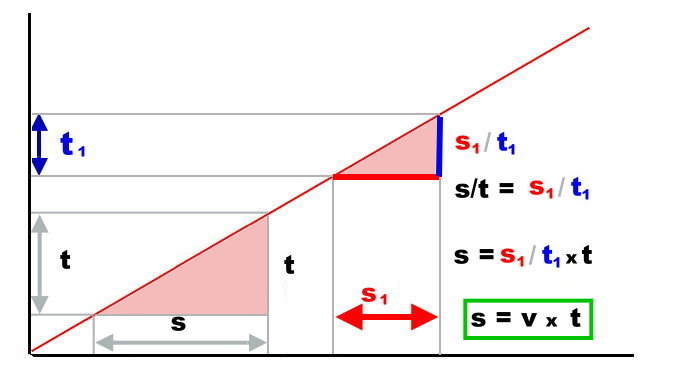
Damit können wir ganz allgemein, für beliebige Werte eine echte Formel aufstellen. s/t ist immer gleich! Diesen Faktor nennen wir in der Physik Geschwindigkeit oder 'velocitas' und nennen ihn fortan immer v. Wohlgemerkt, das ist nur eine Definition. Die aber ganz gut unsere Vorstellungen von diesem Wort trifft.

Auf der linken Seite der Gleichung ist die Angabe in Metern, das t steht für die Zeit in Sekunden. Damit die Gleichung stimmt, muss die Geschwindigkeit einen Wert von Metern/Sekunde haben (m = m/sec * sec). Das macht v richtig plausibel: v sagt, wie viele Meter pro Sekunde zurückgelegt werden (oder Kilometer pro Stunde zum Beispiel). Aber das v hat es in sich, wenn es so als mathematische Größe selbstständig geworden ist: Es verbindet Zeit und Raum auf ganz eigenartige Weise. Ist es nämlich Null, dann ist die Zeit völlig egal. Es kommt für die Veränderung eines Punktes (eines Rades) immer Null heraus oder anders ausgedrückt: Ohne ein v mit einem ordentlichen Wert ändert sich gar nichts. Nichts bewegt sich, nichts verändert sich, da kann man warten, so lange man will. Und wenn das v die Geschwindigkeit des Lichts annimmt, dann wird alles noch eigenartiger. Mehr davon im Kapitel über die Relativitätstheorie.

Jetzt können wir für jede Strecke und jede Zeit ausrechnen, wann sich das Rad wo befindet. Wir können jetzt tatsächlich die Zukunft vorhersagen und das auch noch absolut präzise: In zwei Stunden wird sich das Rad in unserem Beispiel genau 14,4 Kilometer entfernt haben.

Aber die Sache hat einen Haken. Die Geschwindigkeit muss immer gleich bleiben (die Räder auf dem Diagramm immer auf einer geraden Linie sein). Das kommt in der Natur aber nicht immer vor, um genau zu sein: Eher nie. An einer Stelle ist unsere erste Formel jedoch extrem nützlich. Wenn Sie ein Navi oder Maps benutzen, haben sie sicher schon gestaunt, wieso es Ihnen die Ankunftszeit nennen kann. Das geht so: Alle Orte sind in der Datenbank durch eine Strecke verbunden, die nicht nur die Entfernung, sondern auch die mögliche und erlaubte Geschwindigkeit enthält. Hat das Navi einen optimalen Weg gefunden, werden diese Teilabschnitte addiert und daraus die Zeit berechnet. Es handelt sich also dabei um die jeweilige Durchschnittsgeschwindigkeit, die als 'gleichförmig' angenommen wird, für die also unsere obige Formel gilt.

Versetzen Sie sich jetzt ein paar Jahrhunderte zurück. Ein gewisser Herr, namens Galileo Galilei war auf einen Turm gestiegen, sein Assistent hatte eine Uhr dabei. Dann ließ er einen Stein fallen und der arme Assistent musste die Zeiten messen, die der Stein an bestimmten Stellen erreicht hatte. Wie die beiden das genau gemacht haben, wollen wir jetzt einmal beiseite lassen.

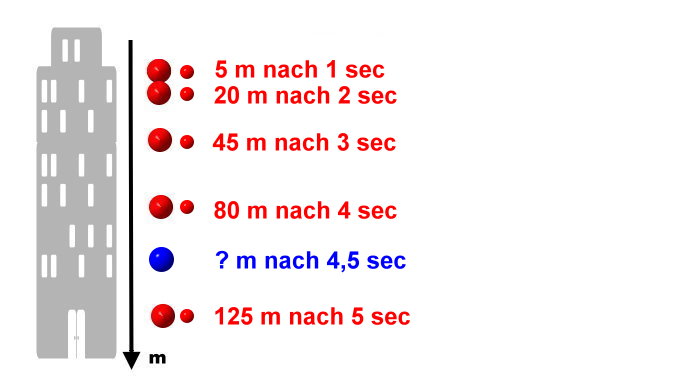
Das Ergebnis war nicht so, wie das mit dem rollenden Rad. (Außerdem war es bemerkenswert, dass auch kleinere Steine exakt gleich schnell fielen. Aber das ist noch eine andere Geschichte). Der Unterschied war sehr schnell zu sehen, als man versucht hatte, die 'Diagramm-Methode' zu benutzen.

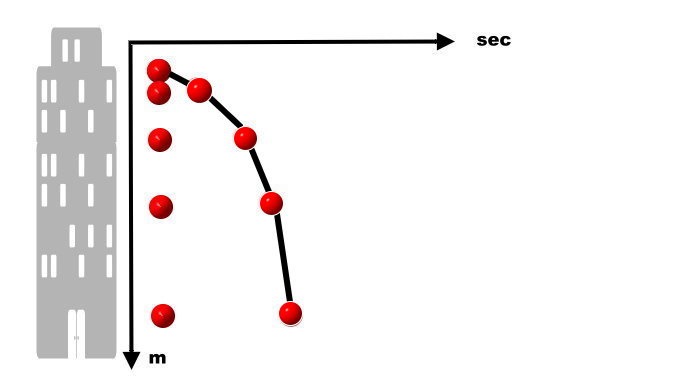
Die Kugeln liegen diesmal nicht auf einer Geraden. Da ist guter Rad teuer. Sie haben lange überlegt. Eines fiel ihnen schon bald auf, als sie die einzelnen Steinpositionen im Diagramm mit geraden Strecken verbanden: Hätte man mehr Messungen gemacht, würde sich der Streckenzug wohl einer weich gebogenen Linie annähern. Das erschien ihnen sehr plausibel. Dieser kleine Gedanke war übrigens ein riesengroßer, auch wenn sie das sicher noch nicht wussten. Er hat die gesamte Mathematik und Physik mit all ihren heutigen Errungenschaften begründet. Gleich mehr davon.

Um bei einem Fall 'die Zukunft' vorhersagen zu können, brauchten sie eine Formel. s/t = v funktioniert ja nicht, weil sich das s/t, also die Geschwindigkeit dauernd verändert. Aber wie zum Teufel tut sie das. Sie haben probiert und probiert. Einer hatte eine Idee: Vielleicht ist das v ja einfach so etwas wie die abgelaufene Zeit, die richtige Formel also s/t = t. In dieser Formel wäre klar, warum die Strecke mit dem Ablauf der Zeit immer größer wird wie im Versuch: s = t x t = t²

Es war eine schöne und einfache Formel. Nur leider stimmten die Messergebnisse nicht mit ihr überein. Wieder hatten sie eine großartige Idee. Wie, wenn wir einfach einen Faktor dazu multiplizierten, eine konstante Zahl. s = k x t². Das war der Druchbruch: Sie fanden eine Zahl und die hat es in sich: Sie galt für alle Körper, eben auch für den kleineren Stein. Das Fallgesetz für den freien Fall war geboren. Der Ehre halber soll erwähnt werden, dass ein gewisser Sir Isaac Newton diese Formel und denFaktor genau berechnet hat. Über die Geschwindigkeit des Steins konnten sie damit aber nichts sagen.

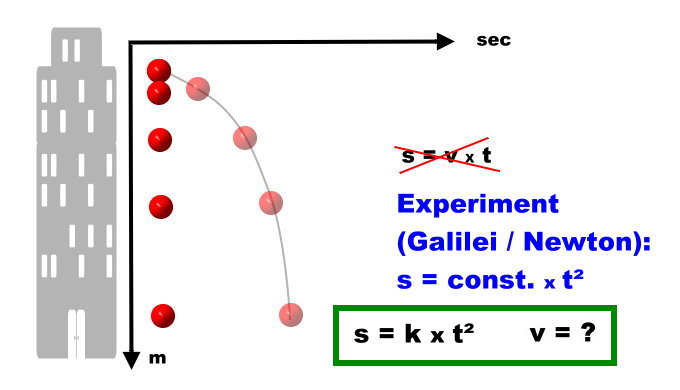
Halten wir fest: Das Ergebnis wurde nicht durch theoretisches Herleiten herausgefunden, sondern durch präzise Experimente und deren mathematische Interpretation. Es hätte auch ganz anders sein können.

Das Ergebnis ist eine Annahme, die druch viele weitere Experimente bestätigt wurde. Erst viel später wurde durch die allgemeine Relativitätstheorie klar, warum es richtig ist. Wobei natürlich auch die Relativitätstheorie eine Annahme ist.

Machen Sie sich bitte einmal klar, was diese Aussage bedeutet: Ein simpler, rein rechnerischer Zusammenhang spiegelt sich in der richtigen Natur so präzise wieder, so dass man damit die Planetenumlaufbahnen, die Mondauf- oder untergänge, den Weg von Raketen, um Satelliten an die richtige Stelle zu bringen, ausrechnen kann. Das ist ein Wunder, denn die Mathematik ist schließlich eine reine Erfindung unseres Gehirns. Die Frage, ob sie auch ohne den Menschen existiert, beschäftigt die Philosophen schon Jahrhunderte ohne Erfolg. Zumal die Mathematik die Natur gar nicht so genau wiederspiegelt, wie es manchmal den Anschein hat. Mehr dazu gleich weiter unten.

Leider konnten sie erst einmal über die Geschwindigkeit nichts sagen. Das wäre aber nötig, nicht nur der Vollständigkeit halber, sondern auch für Berechnungen, zum Beispiel, mit welcher Wucht der Stein auf die Erde auftrifft oder wie eine Kanonenkugel abgefeuert werden muss und viele andere nützliche Betrachtungen.

Ganz allgemein haben wir das Problem, dass die 'Räder' im Diagramm nicht auf einer Geraden liegen. Damit ist unser schöner Faktor, die Geschwindigeit v also abhängig von der Zeit.

Für den speziellen Fall mit dem Steinabwurf, kennen wir aber jetzt die Formel für die Kurve im Diagramm, der der Stein folgt.

Die schon weiter oben aufgeblitzte, geniale Idee wurde von Sir Isaac Newton noch einmal gedacht, die unabhängig von ihm auch ein Herr Gottfried Wilhelm Leibniz im 17. Jahrhundert entwickelte. Sie hat nicht nur zur Lösung dieses Problems verholfen, sondern sie war eine der Sternstunden der Menschheit. Ohne sie wären fast alle unseren technischen Errungenschaften nicht möglich: Die Differential- und Integralrechnung. Beide konnten auch hier die Folgen noch gar nicht erkennen.

Die Idee selbst ist recht einfach: Wenn man einen ganz kleinen Abschnitt einer Kurve betrachtet, kann man sagen, dass die Werte einer geraden Strecke mit der Kurve recht gut übereinstimmen wird, wenn die Strecke die richtige Steigung hat. Mit der Strecke, also einer Geraden können wir die Geschwindigkeit ja schon ausrechnen.

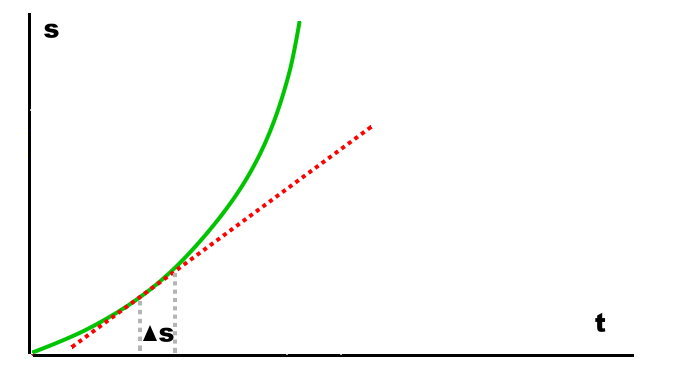
Erschrecken Sie nicht vor diesem Bild. Es ist einfacher, als es aussieht.

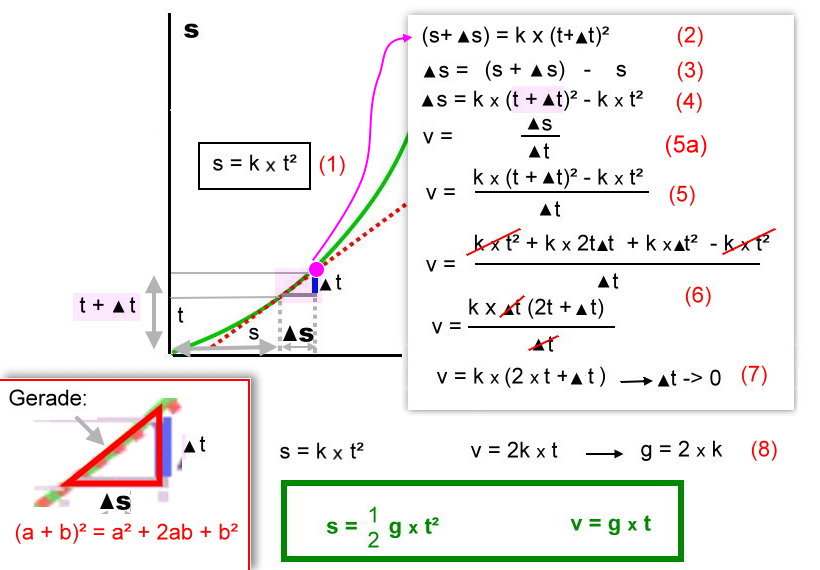
(1) ist die experimentell bestimmte 'Formel' für die Kurve. In (2) ist sie für die Strecke s plus dem kleinen Abschnitt 'delta s' angewendet. Formel (3) ist klar. (4) ist aus (1) und (2) zusammengesetzt gemäß (3). Da für das klitzekleine Geradenstück unsere alte Formel gilt - das ist der Trick dabei - gilt (5a) und damit (5) gemäß (4). (6) ist nur ein bißchen Rechnerei, wobei man wissen muß, dass (a+b)x(a+b) = a x a + a x b + b x a + b x b = a² + 2ab + b² ist. Das ergibt sich einfach aus der Multiplikation der Klammern. (7) ist das Ergebnis dieser Rechnerei. Aber jetzt kommt's: Wir denken uns delta t immer kleiner, die Dreiecke werden zwar auch kleiner, aber es gilt immer noch unsere Annahme mit dem geraden Verlauf der kleinen Strecke. Wird delta t zu Null, dann fällt der Summand einfach weg (a + 0 = a). Übrig bleibt v = 2 x k x t. Jetzt nehmen wir für 2k eine neue Konstante, die doppelt so groß ist, nur damit es schöner aussieht. Wir nennen sie g. Diese Konstante hat den Wert 9,81 m/sec² und nennt sich fortan die Erdbeschleunigung. Sie ist nahe dem Erdboden fast überall gleich groß. Das Wort Beschleunigung ist überdies recht plausibel. Es bedeutet in diesem Falle, dass die Geschwindigkeit des Steins in der Sekunde um 9,81 m/sec zunimmt (m/sec² = m/sec pro Sekunde).

Wir haben damit die Formeln für zwei typische Fälle kennen gelernt, für die wir jetzt genaue Vorhersagen treffen können. Im Laufe der Zeit haben die Mathematiker herausgefunden, dass diese Art des Rechnens ganz einfachen Rechenregeln gehorcht. Das ist eines der weiteren echten Wunder der Mathematik. Man nannte dieses Verhältnis d/dx von einer Funktion f, gesprochen " d nach d t von f ": d/dt(f(t)), die Ableitungvon f.

Die Integralrechnung ist genau die ''Umkehrung'' davon. Die brauchen wir hier aber nicht.

Für unsere gerade Bewegung und für die Erdbeschleunigung gelten also:

Die Rechenregeln sind also für diese Fälle extrem einfach. Nur aus Spaß haben die Mathematiker überlegt, ob es eine Funktion f gäbe, deren Ableitung genau wieder f ist. Gibt es. Nach langem Denken und Rechnen kam man auf die berühmte Eulersche Zahl e. Sie ist eine bemerkenswerte Zahl, die unendlich viele Stellen hat: e = 2.71..... (Man kann sie nicht als Quotient zweier natürlicher Zahlen darstellen, deswegen heißt sie auch 'irrational'. Aber 'reell' ist sie. Immer dann, wenn die Änderung des Wertes (die 'Geschwindigkeitsänderung') vom aktuellen Wert abhängt, die 'Beschleunigung' ist also nicht konstant, dann gilt diese Formel. Sie sagt vorher, warum jemand immer mehr Geld dazu bekommt, je mehr er hat oder warum unsere Bevölkerungszahl auf der Erde dabei ist zu explodieren.

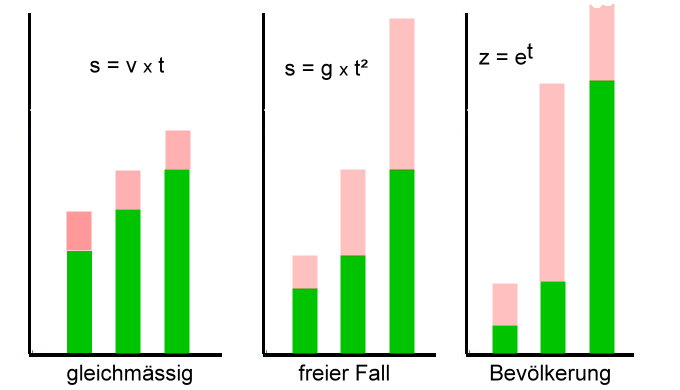
War jetzt recht ausführlich. Und das mit Grund. Fast ausnahmslos beruhen alle Errungenschaften der Wissenschaft und der Technik, wie wir sie heute kennen, auf dieser Methode. Auch, wenn die folgenden, wirklich weltbewegenden Formeln etwas verwirrend aussehen: Es handelt sich nur um eine Abkürzungssprache der Mathematiker. Die Symbole, die sie auf dem nächsten Bild sehen, bestehen immer aus Formeln mit unserem d/dt. (Zum Beispiel steht das Dreieck auf dem Kopf in den Maxwell - Gleichungen für: 'a x d/dx + b x d/dy + c x d/dz'. Weil man das oft braucht, verwendet man die Abkürzung. Mehr ist das nicht.)

Die Schrödingergleichung enthält die fundamentalen Aussagen der Quantenphysik, ohne die unsere modernen Computer oder der Laser nicht entwickelt werden konnte, die Maxwell - Gleichungen haben die Tür aufgestoßen zu allem, was wir heute mit dem Fernseher, dem Smartphone oder dem GPS können und die Gleichung von Einstein hat dazu geführt, dass wir anfangen zu verstehen, wie es mit Raum und Zeit wirklich ist. Aber der praktische Nutzen ist auch im Alltag zu spüren: Vom wirklich scharfen Fernsehbild bis zum Atomstrom und den Solarzellen. Sage keiner, dass Grundlagenforschung reine Geldverschwendung ist. Ohne sie wären wir heute noch in der Welt vor Hunderten von Jahren. Und es gibt keinen Grund anzunehmen, dass wir damit schon am Ende sind.

Jetzt kommen die Problem mit der Mathematik.

Das größte Problem ist, dass sie uns leichtgläubig macht. Wir könnten nämlich auf die Idee kommen, dass wir nur die jeweiligen Formeln kennen müssen, um die Zukunft komplett vorherzusagen. Bei den beiden Beispielen mit der Geschwindigkeit funktioniert das ja ganz gut. Auch in die Vergangenheit können wir genau sehen. Wir brauchen ja nur die Zeit in den Formeln umkehren.

Das hieße also: Kennen wir alle Formeln und für einen einzigen Zeitpunkt die Parameter (wie das g bei der Erdbeschleunigung und den Wert von s zu einem bestimmten Zeitpunkt t), dann können wir für alle Zeiten alle Ergebnisse genau vorhersagen, also die Zukunft. Ein für alle mal und absolut präzise. Zugegeben, das ist schon eine komplexe Aufgabe bei den Abermillionen von Teilchen, die so umherschwirren. Aber grundsätzlich wäre es doch möglich, oder? Mit genügend großen Computern?

Was wäre die Folge? Nun, man könnte einige Katastrophen verhindern, in dem man schon vorher ein paar Parameter ändert. Das wäre toll. Aber halt. Das geht ja gar nicht. Wenn wir die Zukunft so genau berechnen können, dann ist das eben die Zukunft. Da ist kein Raum für Veränderungen. Komisch.

Man hat das schon sehr früh überlegt und diesen ''Supercomputer'' den ''Laplace'schen Dämon''' genannt. (Laplace war ein Astronom und hat Grundlegendes zur Wahrscheinlichkeitsrechnung geleistet. Die er nur dafür erfand, weil er eben nicht alles genau berechnen konnte. Er empfand das als einen bedauernswerten Mangel.) Aber wenn es ihn gäbe, wären die Folgen unabsehbar. Alle Menschen würden sich dem Kismet ergeben, ein freier Wille wäre nur noch eine von einem höhnischen Gott ausgedachte Beruhigungspille. Jedes Eingreifen wäre Illusion, weil alles von Anbeginn (bei der Schöpfung) schon festgelegt wäre.

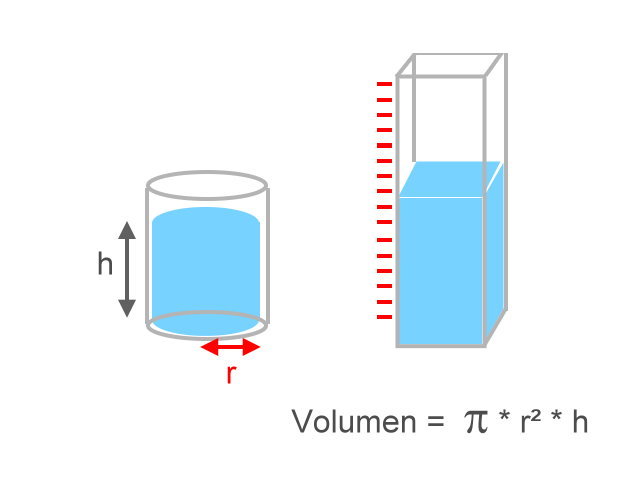
Gottlob haben einige Menschen herausgefunden, dass der Laplace'sche Dämon Humbug ist. Diese Leute haben erst einmal gar nicht über dieses Problem nachgedacht. Sie befassten sich mit Gasen und Flüssigkeiten und merkten sehr schnell, dass die mechanischen Formeln für die einzelnen Teilchen (Atome, Molküle) zwar stimmen mögen, aber praktisch nichts nutzen, weil man mit solchen Mengen nicht rechnen kann. Sie entdeckten einfache Zusammenhänge, die für die übergeordneten Größen wie Druck, Temperatur und Volumen stimmten, die aber nichts darüber aussagten, was die einzelnen Teilchen so treiben. Es war ihnen auch egal. Sie wollten Maschinen erfinden, mit denen man Arbeit leisten konnte. Und das gelang ziemlich gut (die Dampfmaschine oder der Kühlschrank seien als Beispiel genannt).

Heißer Dampf konnte also für mechanischen Antrieb genutzt werden. Da könnte man doch auf die Idee kommen, eine Maschine zu bauen, die Wasser abkühlt und mit der gewonnen Energie Arbeit leistet. Das wäre großartig. Ein Schiff könnte ohne Sprit fahren. Der Motor würde lediglich die Umgebung abkühlen. Kein Problem, die Sonne gleicht das schon wieder aus.

Aber leider, leider, es gelang nicht. Nach langem Probieren gaben sie auf. Sie kamen letztlich auf die Idee, dass da ein grundsätzliches Problem vorliegt und haben es zum berühmten zweiten Hauptsatz der Thermodynamik zusammengefasst. Hier in der Formulierung von Lord Kelvin und Max Planck:

'Es ist unmöglich, eine periodisch arbeitende Maschine zu konstruieren, die weiter nichts bewirkt als Hebung einer Last und Abkühlung eines Wärmereservoirs.'

Dieser Satz ist ein Hammer. Er wirft alles durcheinander, was man bisher geglaubt hat. Und erklären konnte man ihn nicht. Herleiten auch nicht. Er entsprach nur einer (bitteren) Erfahrung. Später fand man zumindest eine etwas genauere Beschreibung. Man erfand einen neuen Begriff: die Entropie. Versuchen Sie nicht, das genau zu begreifen. Ein gutes Bild ist, daß die Entropie ein Maß für die Unordnung in einem System ist und dass die Unordnung viel wahrscheinlicher ist als die Ordnung. Genauer: Geordnete Zustände gibt es wenige, ungeordnete dagegen sehr viele. Mit diesem Begriff lautet der zweite Hauptsatz:

'In einem geschlossenen System kann die Entropie nicht abnehmen, sie nimmt in der Regel zu.'

Auch das ist lediglich eine Erfahrung, die nicht bewiesen ist. Allerdings hat man noch nie das Gegenteil beobachtet. Sie schütten Milch in den Kaffee und rühren um. Die Flüssigkeit wird schön gleichmässig hellbraun. Durch das Rühren wird der Zustand (die Lage der einzelnen Teilchen) ständig verändert. Wie lange müssen sie rühren, bis der Kaffee von der Milch getrennt erscheint (auch das ist ja ein Zustand in der Tasse)? Sie lassen es bestimmt gleich, weil Ihnen die Erfahrung sagt, dass es nicht stattfindet. Der geordnete Zustand ist einfach zu unwahrscheinlich, als dass er irgendwann einmal erscheint. Obwohl das natürlich prinzipiell möglich wäre.

Das führte zu dem geradezu revolutionären Schluss, dass es Prozesse gibt, die nicht mehr rückgängig gemacht werden können. Nehmen wir noch einmal unseren Kaffee zu Hilfe. Wenn wir ihn nämlich stehen lassen, wird er kalt.

Die Umgebung wird wahrscheinlich dadurch etwas wärmer. Aber das Entscheidende ist: Umgekehrt findet das nicht statt. Es kommt nicht vor, dass der Raum abkühlt und der Kaffee wieder warm wird.

Man nennt solche Prozesse irreversibel. Wenn es das gibt - und man kann kaum daran zweifeln - dann ist mit der Umkehr der Zeit in unseren Formeln schon mal nichts. Man kommt nicht zum Ausgangspunkt zurück.

Aber der Blick in die Zukunft bleibt doch, oder? Auch wenn der Milchkaffeee gleichmässig braun ist. Wenn man die Anfangsbedingungen der Teilchen kennt, könnte man das prinzipiell ausrechnen, oder?

Jetzt kommt es ganz Dicke: Es geht nicht. Nicht weil wir noch nicht genug wissen und noch nicht die geeigneten Rechner haben, sondern grundsätzlich. Es ist das der Unterschied zwischen unbekannt und unbestimmt.

Es war halt schon wieder Einstein, der das folgende Beispiel geliefert hat: Wenn wir den Abstoßwinkel, die Anfangsgeschwindigkeit und die Stelle des Abstoßes kennen, können wir ausrechnen, wo sich eine Billardkugel nach einer bestimmten Zeit befindet. Wir müssen nur berücksichtigen, dass der Reflektionswinkel an der Bande dem üblichen Gesetz: Einfallswinkel = Aufallswinkel gehorcht. Das ist grundsätzlich richtig. Aber Einstein wies darauf hin, dass selbst ein kleinster Fehler in den Anfangsbedingungen zu einem unvorhersagbaren Ergebnis führt. Sie sehen das an den folgenden Bildern:

Jetzt nehmen wir eine zweiten Stoß dazu:

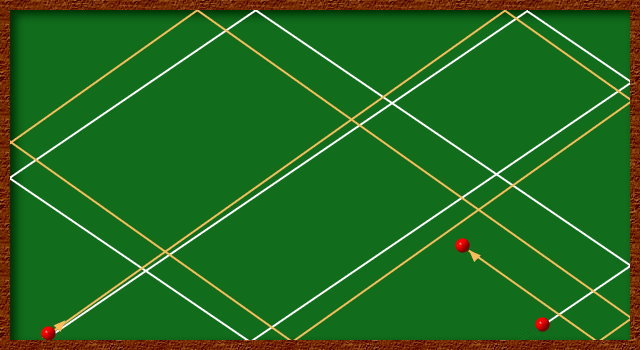
Je nach Fehler kann der Ball im rosa eingefärbten Bereich sein.

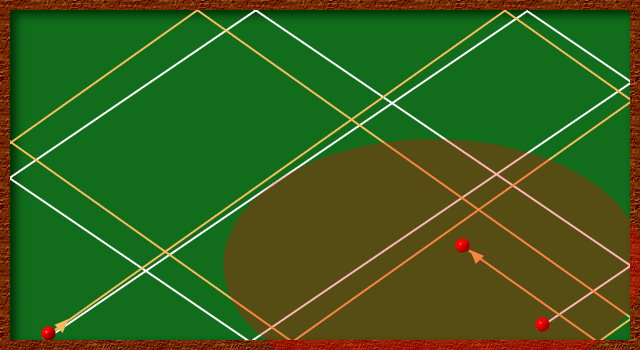
Nehmen wir als Bedingung an, dass wir die Größe möglicher Fehler wissen, dann müssen wir den Weg für die beiden Randwerte berechnen. Damit kann die Kugel in einem weit größeren Bereich liegen.

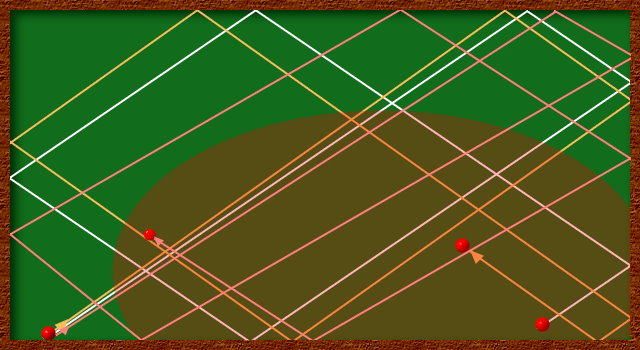
Kein Problem: Denken wir uns eine Vorrichtung aus, die den Fehler kleiner macht... Hilft nichts, die Ungenauigkeit bleibt.

Also darf es eben keinen Fehler geben. Die Kugel muss zum Beispiel genau 8 cm von der linken Ecke starten. Aber was heißt das? Wir nehmen einen Meterstab und messen. Genau 8 können wir nicht sagen, aber zwischen 7,95 und 8,05 cm. Reicht nicht. Also ein besseres Gerät: Wir grenzen den Fehler ein auf 7,99999999 und 8,000000001 und rechnen erneut. Hilft nichts. Wir brauchen genau 8. Jetzt wird es technisch schwierig, weil wir uns bald auf atomarer Größe befinden. Und genau an dieser Stelle kommt die wichtige Frage auf: Wie weit geht denn die Unterteilung? Gibt es beliebig kleine Schritte, die wir jeden wiederum weiter unterteilen können? Abgesehen von der Unmöglichkeit, so ein Meßgerät zu bauen, gibt es da etwas Grundsätzliches: Der Wert hinter dem Komma müsste unendlich viele Stellen haben, um wirklich genau zu sein. Aber was soll das heißen? Unendlich. Und damit: 'wirklich genau'. Dazu müssten wir immer noch kleinere Abschnitte im Raum erkennen können. Das geht aber grundsätzlich nicht. Auch wenn wir immer neuere, noch kleinere Unterteilungen machen können, es gibt immer noch eine weitere dazwischen ( a+b/2 ist immer zwischen a und b). Das Problem bleibt unlösbar.

Was folgern wir daraus? Der Laplace'sche Dämon funktioniert nicht. Nicht, weil wir noch nicht genug wissen, sondern wir die Bedingungen grundsätzlich nicht genau feststellen können.

Nehmen wir noch ein wichtiges Beispiel: Die Wettervorhersage. Da hat der Kachelmann doch etwas Gutes getan. Er hat an möglichst vielen Orten Wetterstationen aufgestellt, um zu jeder Zeit an jedem Ort die wesentlichen Größen festzustellen: Luftdruck, Temperatur und Luftfeuchtigkeit. Mit einem gut fundierten mathematischen Modell, das aus einer einzelnen 'Zelle' die Werte für deren Nachbarzellen berechnet (die Formeln dafür sind recht einfach und stammen von Edward N. Lorenz (nicht zu verwechseln mit Hendrik Lorentz sh. Relativitätstheorie)) sollte man doch das Wetter ein für allemal genau vorhersagen können. Kann man auch, für ein paar Tage. Aber dann geht irgend etwas schief. Die berechneten Kurven sehen ungefähr so aus:

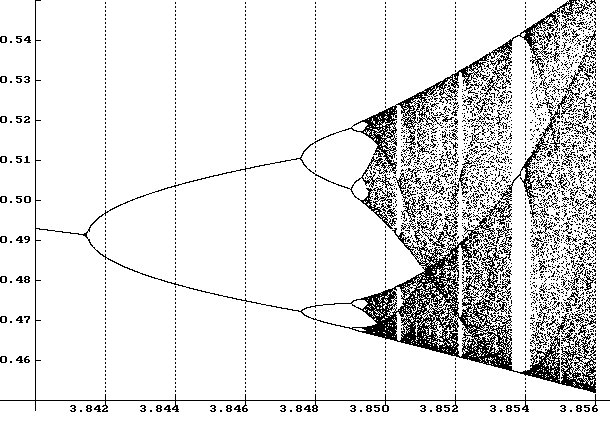
Anfangs ist das recht präzise. Es gibt 'Gabelungen' für die sich der Wert entscheidet, aber plötzlich wird das Ergebnis völlig chaotisch. Was ist da los? Wir kennen die Antwort schon. Es sind die Anfangswerte, die man nicht genau genug angeben kann. Grundsätzlich nicht, wie wir bereits wissen.

Übrigens geschieht mit diesen Werten noch etwas Sonderbares. Liegen sie in bestimmten Bereichen, dann bleiben sie auch für längere Zeit dort. Außerhalb ist das nicht so. Da 'entscheiden' sich die Werte 'plötzlich', zu welcher Bahn sie gehen sollen.

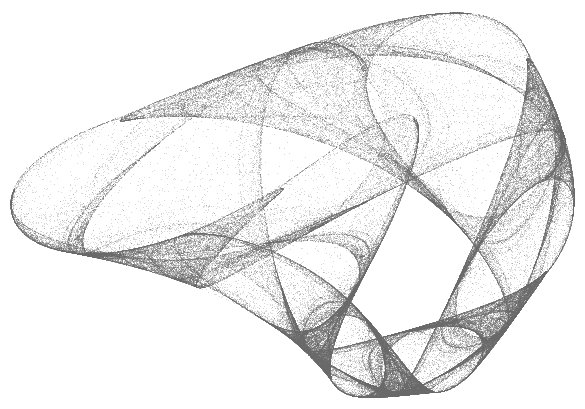
Man nennt diese Kurven zurecht 'seltsame Attraktoren'. Es gibt sie in der Realität. Auch das wissen wir vom Wetterbericht. Manchmal gelingt die Vorhersage wirklich gut, ein anderes Mal berichtet der Wetterexperte, dass man es schlecht vorhersagen kann. Den Grund haben wir gerade gesehen.

Zu komliziert das mit dem Wetter? Gibt es auch einfachere Beispiele? Ja, ein sehr einfaches: Das Doppelpendel.

Wir lenken es ein bisschen aus (mit dem Winkel d und es fängt an zu schwingen. Nach einiger Zeit recht merkwürdig, weil das zweite Pendel sich dauernd nach dem ersten richten muß. Nehmen wir einen klein wenig anderen Winkel, schwingt es anders. Nicht etwa genauso, nur stärker, sondern die Kurve wird völlig anders. Wieder gibt uns ein Diagramm Auskunft:

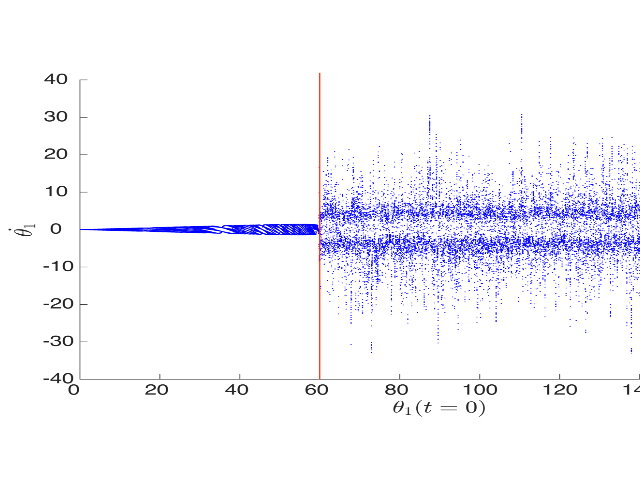
Ab einem bestimmten Winkel wird es völlig chaotisch = nicht mehr berechenbar. Das ist schon merkwürdig. Die Formeln des Pendels sind eigentlich recht einfach und doch... Vorhersagbar ist es wie bei den Billardkugeln nicht. Prinzipiell nicht. Denn die Änderungen des Winkels kann man so klein machen wie man will. Das Ergebnis wird jedes Mal völlig anders sein.

Die Mathematik hat uns aufs Glatteis geführt: Es gibt - wie im Billardbeispiel - nicht genau 8 cm. Die gibt es nur in der mathematischen Vorstellung, in der Realität ist der Begriff sinnlos und zwecklos.

Diese Erkenntnis führt uns sofort auf eine neues Problem: Ist der Stoß der Billardkugel oder das Doppelpendel und seine tatsächliche Bahn (die wir ja sehen können) eine zufällige Sache oder fehlen uns nur 'verborgene' Parameter? So bald aber auch diese physikalisch von Bedeutung wären, unterliegen sie dem gleichen Problem. Gibt es also den echten Zufall?

Nehmen wir das Würfeln. Wenn Sie den Einwand haben, man kann Würfe manipulieren durch die Ausgangslage in der Hand und eine ausgeklügelte Feinmotorik oder durch eine Inhomogenität des Würfels selber, dann machen wir es anders: Sechs gleiche Kugeln mit den Ziffern 1 - 6 kommen in einen schwarzen Sack und jeweils eine wird herausgenommen.

Auch hier passiert etwas sehr Merkwürdiges. Macht man das oft genug, so wird das Ergebnis immer näher an die Gleichverteilung kommen. Ganz locker könnte man sagen, es sei eben sehr unwahrscheinlich, dass hundert Mal die 6 gewürfelt wird. Aber so einfach ist das nicht. Eigentlich hat man noch keine Erklärung dafür. Man weiß lediglich, dass sich die Gleichheit einstellt. Nimmt man mehrere Würfel und zählt die Augen zusammen, so wird das Diagramm anders. Es bildet sich eine Glockenkurve heraus (sie heißt Gauß'sche Glockenkurve). Gauß hat sich viel damit beschäftigt, weil er hinter den Mechanismus kommen wollte. Die Formel für die Normalverteilung kam heraus.

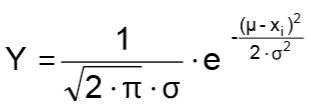
Diese Formel erklärt keineswegs das Phänomen, aber sie liefert eine zuverlässige Vorhersage für Wahrscheinlichkeiten. Am folgenden Diagramm sehen Sie die Entwicklung der Werte mit mehreren Würfeln.

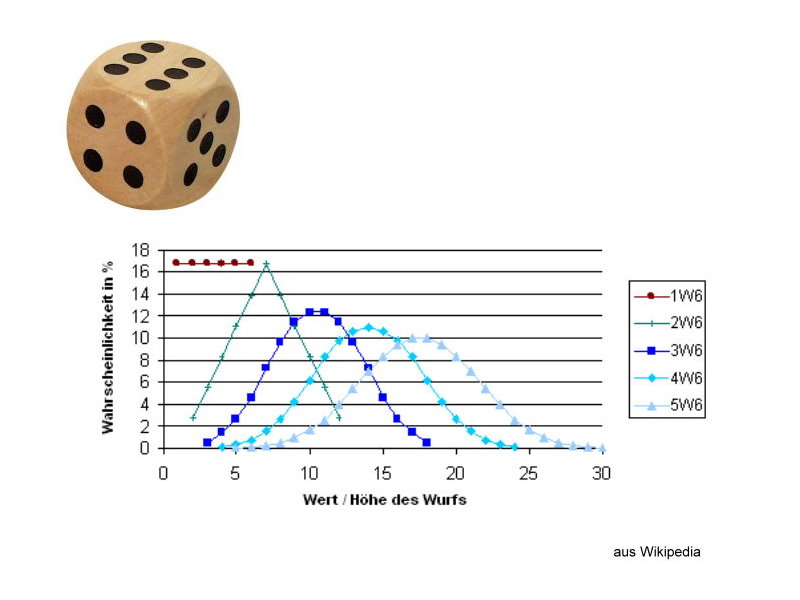
Das Erreichen des Gauß'schen Kurve ist übrigens leicht verständlich, wenn man die Gleichverteilung akzeptiert hat. 3 + 4 + 1 = 8 oder 5 + 1 + 2 = 8 oder 1 + 6 + 1 = 8. Viele Kombinationen führen zum selben Summenwert, aber nur 1 + 1 + 1 zu 3 und 6 + 6 + 6 zu 18.

Wir haben gesehen, dass die Mathematik keine zuverlässige Kristallkugel ist. Aber wenn wir sie richtig einsetzen und nicht von ihr erwarten, dass sie uns die Zukunft vorhersagt, so wie wir das gerne hätten, dann ist sie ein überaus mächtiges Instrument, das jede Menge Überraschungen liefert und uns darauf aufmerksam macht, dass in der Welt nicht alles so ist, wie wir zu sehen glauben. Im Gegenteil, die Welt ist sehr, sehr eigenartig. Nehmen Sie einen Papierstreifen und kleben ihn am Ende um 180° verdreht zusammen. Na und, werden Sie sagen. Kann man machen. Dann gehen sie mit dem Finger am Streifen entlang. Schnell wird Ihnen klar, was passiert ist: Das Band hat keine Ober- und Unterseite mehr. Sie kommen nach einiger Zeit an und haben dabei alle 'Seiten' durchwandert, ohne die Seiten gewechselt zu haben.

Kann doch gar nicht sein, oder? Ein Band hat eine Ober- und eine Unterseite. Dieses nicht. Es hat tatsächlich nur noch eine Seite. Keine Sorge: Unser Gehirn kann damit nicht zurecht kommen. Aber es kann das Möbiusband erfinden.

Eine andere, im Grunde unerklärliche Sache ist die Erkenntnis, dass der Umfang eines Kreises immer proportional zum Radius ist, die Fläche zum Quadrat des Radius. Die Griechen haben diese Zahl entdeckt, als sie versuchten, eine Kreisfläche durch geometrische Konstruktion eines passenden Quadrats zu berechnen. Die Quadratur des Kreises hat nicht funktioniert. Also hat man es durch Annäherung probiert und immer mehr Vielecke eingezeichnet, deren Fläche man ja leicht berechnen kann. Herausgekommen ist dabei die berühmte 'Zahl' p.

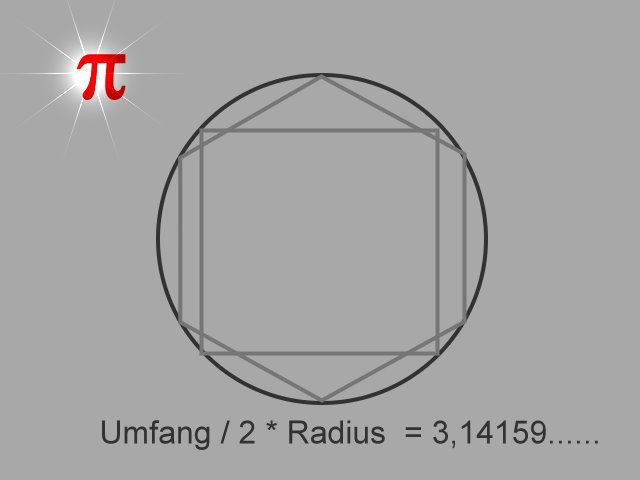
Das ist schon eine sehr merkwürdige Zahl. Bis dahin hatte man gedacht, dass man jede Zahl als Bruch zweier natürlicher Zahlen darstellen kann. Diese sogenannten 'rationalen Zahlen' sind nämlich völlig 'dicht' im Zahlenraum. Dicht heißt in der Mathematik 'lückenlos'. Nehmen sie zwei beliebige Zahlen, a und b, dann liegt (a+b)/2 genau dazwischen. Da man das für jedes a und b machen kann, auch wenn beide 'ganz nahe' beieinander liegen, gibt es also keine Lücken. Gibt es wohl doch. Man konnte nämlich kein Paar von Zahlen finden, mit der sich das 'Pi' als a/b darstellen lässt. Man konnte soger beweisen, dass es ein solches Zahlenpaar gar nicht geben kann. Die Zahl ist 3.14159..... Man hat sie heute auf Millionen von Stellen hinter dem Komma berechnet. Nie wiederholt sich eine Sequenz, was die Voraussetzung wäre, die Zahl als Quotient darzustellen. Dabei kann jeder das Pi selbst experimentell herausfinden:

Aber eben nicht genau. Aber das kennen sie ja schon.

Letztlich bleibt nur übrig, immer weiter zu forschen und damit immer neue technische Fortschritte zu erzielen. Aber bitte mit dem Bewußtsein, das vieles, wenn nicht das Wesentliche geheimnisvoll und unerreichbar bleibt.

Ist Ihnen eigentlich klar, dass es den Kreis gar nicht gibt?

Der Kreis ist eine Erfindung des Gehirns. Er kommt nicht vor. Es gibt ihn nicht, sozusagen. Auch das obige Bild ist kein Kreis. Der Computer hat es gezeichnet, aber wegen der Pixel und unvermeidbaren Verzerrungen ist es nur eine grobe Annäherung an das, was wir einen Kreis nennen. Aber die Idee eines Kreises, die gibt es, zweifelsohne.